The org.orekit.orbits package provides classes to represent orbits.
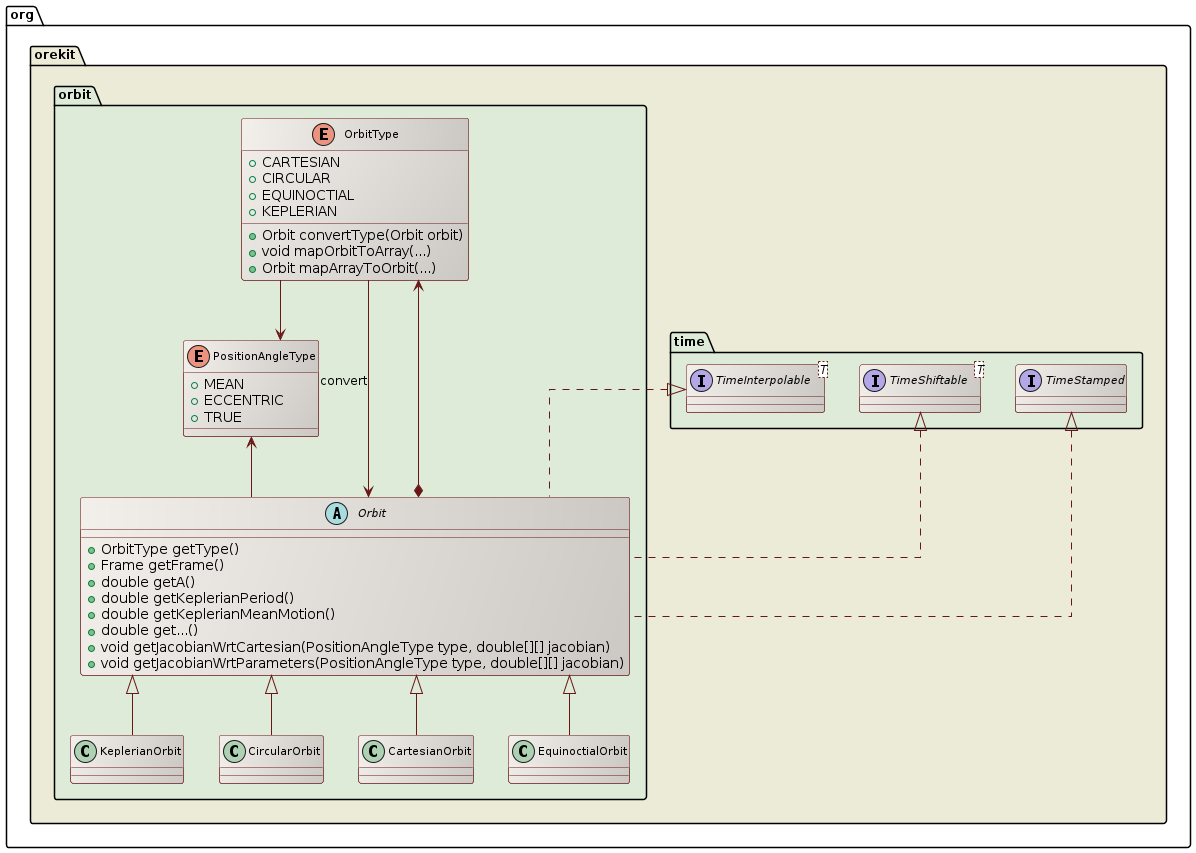
This package is the basis for all of the other space mechanics tools. It provides an abstract class, Orbit, extended in four different ways corresponding to the different possible representations of orbital parameters. Since version 3.0, Keplerian, circular, equinoctial and Cartesian representations are supported.
Early designs for the orbit package were much more complex than the current design. Looking back at these designs, they tried to do far too much in a single class and resulted in huge systems which were difficult to understand, difficult to use, difficult to maintain and difficult to reuse. They mixed several different notions:
They also often neglected all frames issues.
The current design has been reached by progressively removing spurious layers and setting them apart in dedicated packages. All these notions are now still handled, but all in different classes that are cleanly linked to each other. Without knowing it, we have followed Antoine de Saint Exupéry's saying:
It seems that perfection is reached not when there is nothing left to add, but when there is nothing left to take away.
The current design is not perfect, of course, but it is easy to understand, easy to use, easy to maintain and reusable.
From the early design, the various orbit classes retained only the kinematical
notions at a single time. They basically represent the current state, and
serve as data holders. Most of the methods provided by these orbits classes are
getters. Some of them (the non-ambiguous ones that must be always available) are
defined in the top Orbit abstract class (Orbit.getA(), Orbit.getDate(),
Orbit.getPVCoordinates()). The more specific ones depending on the type of
representation are only defined in the corresponding class
(CircularOrbit.getCircularEx() for example).
It is important to note that some parameters are available even if they seem out of place with regard to the representation. For example the semi-major axis is available even in Cartesian representation and the position/velocity even in non-Cartesian representation. This choice is a pragmatic one. These parameters are really used in many places in algorithms, for computation related to period (setting a convergence threshold or a search interval) or geometry (computing swath or lighting). A side-effect of this choice is that all orbits do include a value for µ, the acceleration coefficient of the central body. This value is only used for the representation of the parameters and for conversion purposes, it is not always the same as the value used for propagation (but of course, using different values should be done with care).
Orbits also include a reference to a date and a defining frame. Only pseudo-inertial frames can be used to define orbits, as Newtonian mechanics should apply within the context of the frame. Including frames allows transparent conversions to any other frames at given date, without having to externally preserve a mapping between orbits and their frame: it is already done. As an example, getting the position and velocity of a satellite given by a circular orbit in a ground station frame is simply a matter of calling orbit.getPVCoordinates(stationFrame), regardless of the pseudo-inertial frame in which the orbit is defined (EME2000, GCRF …).
Since orbits are used everywhere in space dynamics applications and since we have chosen to restrict them to a simple state holder, all orbit classes are guaranteed to be immutable. They are small objects and they are shared by many parts. This change was done in 2006 and tremendously simplified the library and the users applications that were previously forced to copy orbits as an application of defensive programming, and that were plagued by difficult-to-find bugs when they forgot to copy.
For orbit evolution computation, this package is not sufficient. There is a need to include notions of dynamics, forces models, propagation algorithms … The entry point for this is the Propagator interface.
Available orbit representations are :
Classic elliptical Keplerian orbit, which parameters are :
Circular orbit, used to represent almost circular orbit, i.e orbit with low eccentricity. Its parameters are:
Equinoctial orbit, used to represent equinoctial orbits (almost circular orbit with almost null inclination). Its parameters are:
Cartesian orbit, associated to its frame definition, the parameters for which are:
Note that Two-Lines Elements are not considered orbits representation here. This is because TLE are in fact a merge between orbital state and a propagation model. The state is only meaningful with respect to the associated SGP4/SDP4 propagation model, and cannot be used in any other model.
All representations can be converted into all other ones. No error is triggered if some conversion is ambiguous (like converting a perfectly circular orbit from Cartesian representation to Keplerian representation, with an ambiguity on the perigee argument). This design choice is the result of many different attempts and pragmatic considerations. The rationale is that from a physical point of view, there is no singularity. The singularity is only introduced by a choice of representations. Even considering this, it appears that rather than having a parameter with no realistic value, there is an infinite possible number of values that all represent the same physical orbit. Orekit simply does an arbitrary choice, often choosing simply the value 0. In our example case, we would then get a converted orbit with a 0 perigee argument. This choice is valid, just as any other choice (π/2, π, whatever …) would have been valid, in the sense that it does represent correctly the orbit and when converted back to the original non-ambiguous representation it does give the right result.
We therefore consider it the responsibility of the user to be aware of the correct definition of the different representations and of the singularities relative to each one of them. If the user really needs to do some conversion (for example to provide an orbit as Two-Line Elements later on, remembering that TLEs do use Keplerian-like parameters), then he can do so.
The way conversion is handled in Orekit is very simple and allows easy and transparent processing, while avoiding blindly creating a new object if the the original orbit was already of the appropriate type. So the appropriate way to convert an orbit is the following one, using CircularOrbit as an example:
OrbitType type = OrbitType.CIRCULAR;
CircularOrbit circular = (CircularOrbit) type.convertType(orbit);
In this example, the cast to CircularOrbit is garanteed to succeed because the type enumerate is CIRCULAR. No object will be created if orbit was already the proper type. As an example, the Eckstein-Hechler propagator is defined in terms of circular orbit only. So there is an implicit conversion done at propagator initialization or reset state time, using internally a code similar to the example above.