Tessellation
This package provides tools to discretize geographical zones defined over an ellipsoid.
Overview
Earth observation missions often need to evaluate some properties globally over a geographic zone.
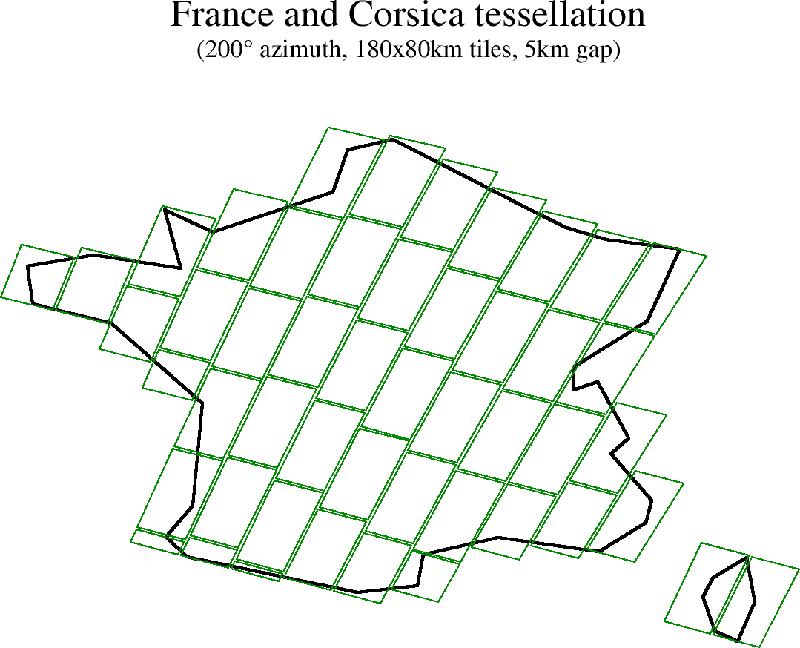
One typical uses are to tessellate a zone of interest in order to define a set of different tiles that will be observed at different times. Using events detection, the precise date at which each tile can be observed is determined and can be uploaded to the spacecraft. Once all tiles have been observed, they are stitched back together to have a full composite image.
Another usage is to sample a zone of interest in order to create a grid and then compute the Dilution Of Precision for a navigation application on each grid point.
Zone Of Interest Definition
The definition of the zone of interest is done using Hipparchus
SphericalPolygonsSet class, which can handle arbitrarily complex area.
It is possible to use non-connected area (for example an archipelago with
separated islands). It is possible to use are with holes (for example to
defined a zone limited to coastal waters and ignoring the internal land
masses).
The zone of interest should not be too large. This tessellation feature is intended only for parts of the ellipsoid. The reason for the limitation is that tiles/grids are computed step by step starting from a seed point (determined automatically), and moving along perpendicular arcs in the along and across tile/grid cell. This gives accurate results locally but fail on a global scale. Attempts to use this on a half sphere is prone to failing badly. Large zones of interest should be split in smaller parts before this feature is used on the parts.
As the SphericalPolygonsSet class is based on the unit 2-sphere, some
convention had to be used to map the ellipsoid to it. The convention
adopted is to preserve the geodetic latitude and longitude, as they
are the ones used in geographical maps. This means that in order to
convert a GeodeticPoint into a S2Point as used by SphericalPolygonsSet,
the following statement should be used:
S2Point s2 = new S2Point(geodeticPoint.getLongitude(),
0.5 * FastMath.PI - geodeticPoint.getLatitude())
The EllipsoidTessellator class provides helper static methods to build
SphericalPolygonsSet from geodetic points defining the zone of interest
boundary in the simple case the zone is path-connected and without holes.
Care should be taken with the points ordering as they are expected to surround
the zone counterclockwise (i.e. the interior is on the left hand side as
we travel from one point to next point). Wrong orientation implies that
what is defined is the complement of the desired region, which is much
larger and will certainly fail to be tessellated properly as per the
limitation explained above.
More complex zones can be built from simple ones using the set operations
available in Hipparchus RegionFactory class (union, intersection,
differences, symmetric difference, complement).
Tile aiming
Depending on the needs of the calling application, different main directions can be used for tile aiming. Two classical orientations are predefined:
-
along track aiming: This mode is used when the user wants to have tiles aligned along the track of a satellite.
-
constant azimuth aiming: This mode is used when the user wants to have tiles aligned at some fixed azimuth with respect to ground point geographic North.
Users can provide their own implementation of the TileAiming interface in addition to
the two predefined directions.
Tessellation and Sampling
There are two main operations that can be performed on zones of interest: tessellation and sampling.
Tessellation produces tiles, which are used when surface-related elements are needed. The tiles created completely cover the zone of interest.
Sampling produces grids of points, which are used when point-related elements are needed. The points created lie entirely within the zone of interest.
In both cases, two dimensions are used, the length of the tile along the tile/grid cell along direction and the width in the across direction. These dimensions are expressed in meters and correspond to a path along the ellipsoid. The local curvature of the ellipsoid is used to move from one point to the next one. As neither the ellipsoid nor the sphere are developable surfaces, the farthest we move from the initial point the more deformation we will experience. This explains the limitation on the size of the zone expressed above.
In the case of tiles, it is also possible to specify an overlap (or gap) between adjacent tiles, both in the along and across directions. It is also possible to tessellate with tiles having all the same dimensions (which will be roughly balanced around the zone of interest) or to tessellate more tightly, with the first column (resp. row) placed wery close to the zone boundary and the last column (resp. row) reduced in width (resp. length).
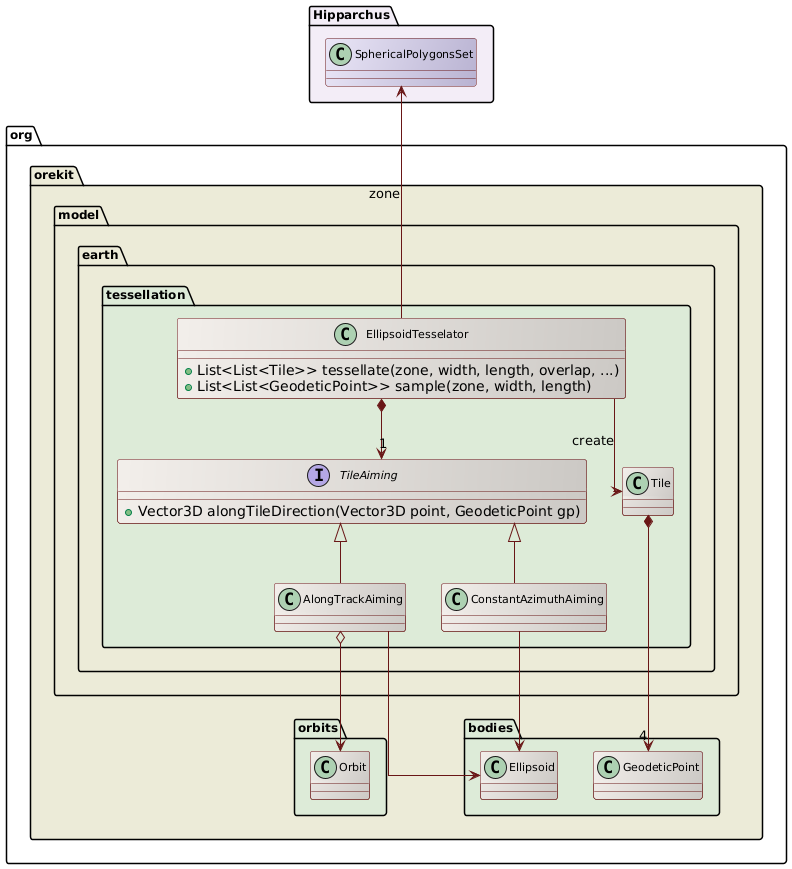
Class diagram
The following class diagram shows the overall design of the package.